BirdLife Rogaland
Drittpreik om kråker ved Mosvatn
Bjørn H. Auestad er statistiker ved Universitetet i Stavanger. Han har, som et undervisningseksempel til elevene sine, regnet på hvor sannsynlig det er bli bæsjet på av kråkefugler under en joggetur rundt Mosvatn. Som vist er sannsynnligheten for å bli truffet heller liten, til tross for et stort antall fugler på et lite område. Ikke bare joggere kan bli truffet av bæsj. Det blir sett vinterkråker om dagen i Stavanger sentrum som er ganske tilgriset av ekskrementer. Dette har vært fugler i god kondisjon, og som sannsynligvis har blitt bæsjet på av artsfrender i Mosvatnet om natten. Så her gjelder kanskje kommentaren: Top guys looking down only see shitheads; bottom guys looking up only see assholes…” Les den drittinterressante sannsynlighetsberegningen for sjansene for å bli truffet av kråkedritt på joggetur rundt Mosvatn!
Av Bjørn H. Auestad, Øyvind Gjerde og Martin Eggen
Publisert 24.03.2013
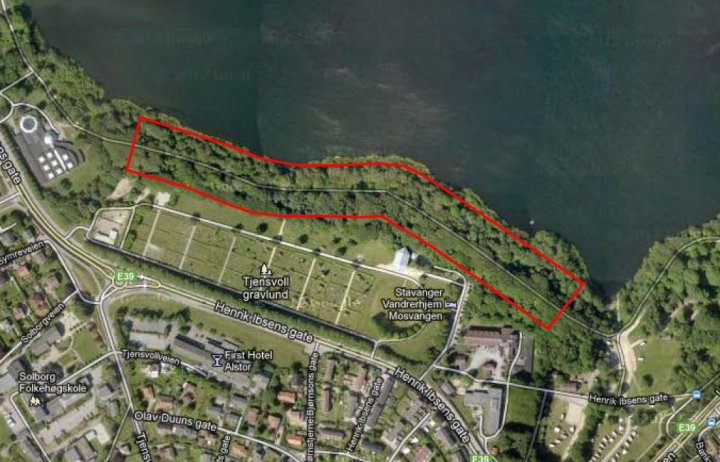
- 24 000 (18 000 + 6 000) kråker og kaier sitter jevnt fordelt i et belte mellom Mostun og Mosvangen.
Vi sier turstien på denne strekningen er 600m lang (ikke langt fra virkeligheten),
og vi sier fuglene sitter i et 40m bredt belte langs stien. Da har vi i gjennomsnitt
en fugl pr. m2.
- Dersom vi sier at fuglene bæsjer i gjennomsnitt tre ganger mellom 17 og 23, kan vi
altså forvente tre bæsjer pr. m2 i løpet av perioden 17 og 23. En del av disse treffer greiner
og kompiser som sitter lavere. Så kanskje vi skal si at vi kan forvente to bæsjer pr. m2 i perioden? - Vi kan forenkle videre og sier at bæsjen faller rett ned (den som ikke treffer noe annet).
Altså, vi tar ikke hensyn til effekter av vind og lignende.
(Vi ser også bort fra at vindforholdene antakelig påvirker hvor i trærne fuglene setter seg; flest nærmere vannet, eller motsatt.)
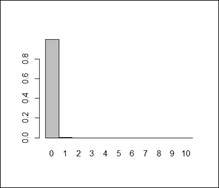
En rimelig sannsynlighetsmodell vil så langt være å si at antall bæsj som treffer et areal
på a m2 i løpet perioden 17-23, er poissonfordelt med forventning 2*a. For a=1 m2 vil vi
da ha sannsynlighetsfordelingen (poissonfordeling med forventning 2): Figur 1
- Sett fra fuglen sitt synspunkt utgjør jeg som blink et areal på omtrent 0.2m x 0.6m = 0.12m2.
- Dersom jeg jogger i en fart av 5min/km, bruker jeg 3 minutter på det utsatte strekket
på 600 meter. Jeg vil da på en runde være utsatt i kun 3 minutter av de 6 timene mellom
17 og 23. Dvs. at jeg eksponeres i 1/120 av tiden mellom 17 og 23.
I og med at vi har tenkt en gjennomsnittlig jevnt fordelt intensitet av bæsj, trenger vi ikke ta hensyn til at jeg beveger meg. Det er nok å ta hensyn til hvor lenge jeg oppholder meg i «risikosonen». - Forventet antall treff på meg (0.12m2) i løpet av 3 minutt kan da anslås til: 2 x 0.12 x (1/120)
= 0.002. Poissonfordelingen for dette ser slik ut ( ):
- Jeg mener jeg er truffet to ganger gjennom tidene. Det kan godt stemme at jeg har jogget et sted mellom 500 og 1500 ganger rundt i løpet av 10-20 år (1/uke, 45 uker/år, 15år = 675).
- Dersom fuglene i gjennomsnitt bæsjer sjeldnere, blir det mindre sannsynlighet, og dersom fuglene fordeler seg på en måte i trærne slik at det i gjennomsnitt er mindre enn en fugl pr. m2, så blir også sannsynligheten mindre. Dersom det for eksempel i gjennomsnitt er bare en fugl pr to m2 (og alt annet likt), blir sannsynligheten halvert.
- Sannsynligheten avhenger av farten man beveger seg i som vi har sett. I våre regnestykker fordi det bestemmer hvor lenge i oppholder oss i «risikosonen». Det kan jo også tenkes at dersom vi løper veldig fort, vil vi få en viss sannsynlighet for «å løpe på» en fallende bæsj som ved saktere fart ville ha truffet bakken foran oss. Slike tinger det ikke tatt hensyn til i regnestykket, men det vil neppe være av vesentlig betydning.
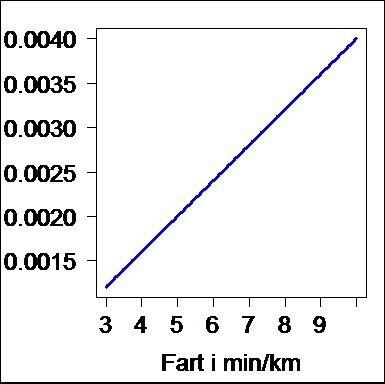
- Sannsynlighet som funksjon av joggefart: Dersom vi ser bort fra «løpe på»-risikoen som nevnt over, vil det å ha større fart når man jogger gi mindre sannsynlighet for å bli truffet. I eksempelet over regnet vi med farten 5min/km. Vi kan se hvordan sannsynligheten endres som funksjon av farten mellom 3 og 10min/km ( som er omtrent gåfart). Figuren 2 framstiller dette med fart på x-aksen og sannsynlighet på y-aksen.